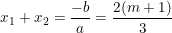tìm m để phương trình có nghiệm thuộc khoảng lớp 10

Trang chủ Tin tức mới Kiến thức THPT Trung Học PT lớp 10 Môn Toán 10 Cách giải phương trình bậc 2 chứa tham số m – Toán lớp 10

Giải phương trình bậc 2 có chứa tham số m là dạng toán biện luận đòi hỏi kỹ năng bao quát tổng hợp, vì vậy mà dạng này gây khá nhiều bối rối cho rất nhiều em.

Đang xem: Tìm m để phương trình có nghiệm thuộc khoảng lớp 10

Vậy làm sao để giải phương trình có chứa tham số m (hay tìm m để phương trình có nghiệm thỏa điều kiện nào đó) một cách đầy đủ và chính xác. Chúng ta cùng ôn lại một số nội dung lý thuyết và vận dụng giải các bài toán minh họa phương trình bậc 2 có chứa tham số để rèn kỹ năng giải dạng toán này.

° Cách giải phương trình bậc 2 có chứa tham số m

¤ Nếu a = 0 thì tìm nghiệm của phương trình bậc nhất

¤ Nếu a ≠ 0 thì thực hiện các bước sau:

– Tính biệt số Δ

– Xét các trường hợp của Δ (nếu Δ có chứa tham số)

– Tìm nghiệm của phương trình theo tham số

* Ví dụ 1: Giải và biện luận phương trình sau theo tham số m: 3×2 – 2(m + 1)x + 3m – 5 = 0 (*)

° Lời giải:

– Bài toán có hệ số b chẵn nên thay vì tính Δ ta tính Δ”. Ta có:

Δ”= <-(m + 1)>2 – 3.(3m – 5)

  = (m + 1)2 – 9m +15 > 0

  = m2 + 2m + 1 – 9m + 15

  = m2 – 7m + 16 > 0

  = (m – 7/2)2 + 15/4 > 0

– Như vậy, Δ” > 0, ∀m ∈ R nên phương trình (*) luôn có 2 nghiệm phân biệt:

* Ví dụ 2:  Giải và biện luận phương trình sau theo tham số m: mx2 – 2(m – 2)x + m – 3 = 0 (*)

° Lời giải:

• TH1: Nếu m = 0 thay vào (*) ta được:

• TH2: m ≠ 0 ta tính biệt số Δ” như sau:

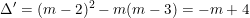
– Nếu 

: Phương trình (*) vô nghiệm

– Nếu 

: Phương trình (*) có nghiệm kép: 

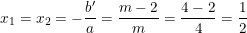
– Nếu 

: Phương trình (*) có 2 nghiệm phân biệt:

¤ Kết luận:

 m > 4: Phương trình (*) vô nghiệm

 m = 0: Phương trình (*) có nghiệm đơn x = 3/4.

 m = 4: Phương trình (*) có nghiệm kép x = 1/2.

 m < 4 và m ≠ 0: Phương trình (*) có 2 nghiệm phân biệt 

* Nhận xét: Như vậy các em cần lưu ý khi tham số nằm ở phần hệ số của ẩn bậc 2 thì ta phải xét thêm trường hợp hệ số ẩn bậc 2 bằng 0 trước khi tính biệt số Δ (Δ”).

– Thông thường, phương trình bậc 2 có chứa tham số thường đi kèm với nhiều bài toán phụ như: Tìm m để phương trình bậc 2 (ax2 + bx + c = 0) có nghiệm thỏa mãn điều kiện nào đó.

* Với 

 thì PT bậc 2:

– Có nghiệm (có hai nghiệm) ⇔ Δ ≥ 0

– Vô nghiệm ⇔ Δ < 0

– Nghiệm duy nhất (nghiệm kép) ⇔ Δ = 0

– Có 2 nghiệm phân biệt ⇔ Δ > 0

– Có 2 nghiệm cùng dấu

– Có 2 nghiệm trái dấu 

– Có 2 nghiệm dương (x1, x2>0) 

– Có 2 nghiệm âm (x1, x2<0) 

– Có 2 nghiệm phân biệt đối nhau 

– Có 2 nghiệm phân biệt là nghịch đảo của nhau 

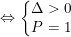
– Có 2 nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn 

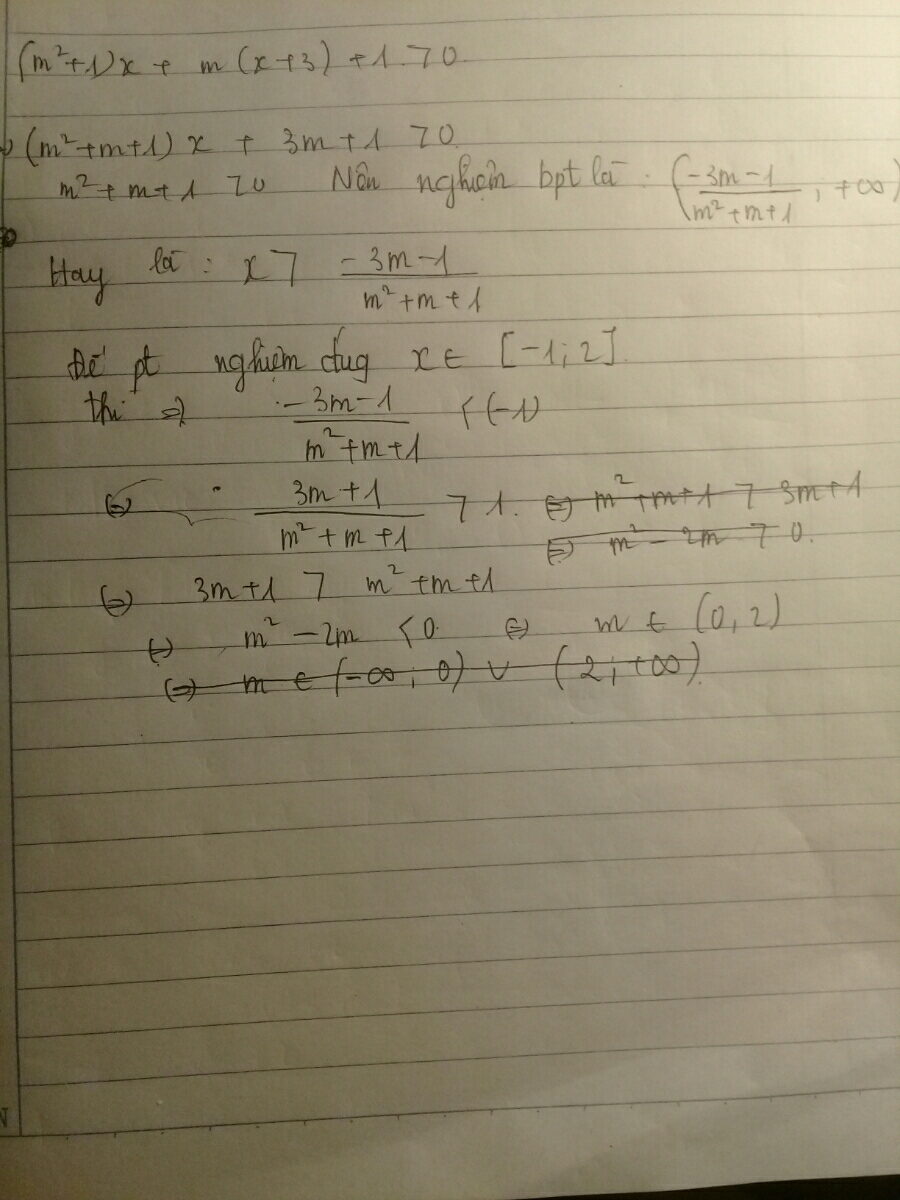
– Có 2 nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối nhỏ hơn 

• Điều kiện để phương trình có 2 nghiệm phân biệt sao cho x1 = px2 (với p ∈ R). Các bước làm như sau:

 Bước 1: Tìm điều kiện để pt có 2 nghiện phân biệt

 Bước 2: Áp dụng Vi-ét tìm: 

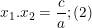
 Bước 3: Kết hợp (1) và giả thiết giải hệ: 

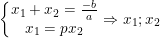
 Bước 4: Thay x1, x2 vào (2) ta tìm được giá trị tham số.

* Ví dụ (Bài 8 trang 63 SGK Đại số 10):  Cho phương trình 3×2 – 2(m + 1)x + 3m – 5 = 0

Xác định m để phương trình có một nghiệm gấp ba nghiệm kia. Tính các nghiệm trong trường hợp đó.

° Lời giải:

– Ta có : 3×2 – 2(m + 1)x + 3m – 5 = 0 (1)

– PT (1) có hai nghiệm phân biệt khi Δ’ > 0

 ⇔ <-(m + 1)>2 – 3.(3m – 5) > 0

 ⇔ (m + 1)2 – 9m +15 > 0

 ⇔ m2 + 2m + 1 – 9m + 15 > 0

 ⇔ m2 – 7m + 16 > 0

 ⇔ (m – 7/2)2 + 15/4 > 0 (∀m ∈ R).

⇒ Phương trình (1) luôn có hai nghiệm phân biệt. Gọi hai nghiệm đó là x1; x2 khi đó theo định lý Vi–et ta có:

 (1); và 

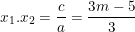
 (2)

– Theo bài toán yêu cầu PT có một nghiệm gấp ba nghiệm kia, giả sử x2 = 3.x1, khi đó thay vào (1) ta có: 

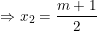
Thay x1, x2 vào (2) ta được: 

* TH1: Với m = 3, PT(1) trở thành 3×2 – 8x + 4 = 0 có hai nghiệm x1 = 2/3 và x2 = 2 thỏa mãn điều kiện.

* TH2: Với m = 7, PT(1) trở thành 3×2 – 16x + 16 = 0 có hai nghiệm x1 = 4/3 và x2 = 4 thỏa mãn điều kiện.

⇒ Kết luận: m = 3 thì pt có hai nghiệm là 2/3 và 2; m = 7 thì pt có hai nghiệm 4/3 và 4.

• Điều kiện để phương trình có 2 nghiệm thỏa mãn điều kiện |x1 – x2| = k (với k ∈ R). Các bước làm như sau:

 Bước 1: Bình phương 2 vế phương trình: (x1 – x2)2 = k2 ⇔ (x1 + x2)2 – 4x1x2 = k2

 Bước 2: Áp dụng Vi-ét tính x1 + x2 và x1.x2 thay vào biểu thức trên được kết quả.

* Ví dụ: cho phương trình x2 – (2m – 1)x + m2 – 1 = 0 (m là tham số).

Xem thêm: Khóa Học Nắm Bắt Tâm Lý Khách Hàng Giúp Nâng Cao Hiệu Quả Kinh Doanh

a) Tìm điều kiện m để pt đã cho có 2 nghiệm phân biệt

b) Xác định giá trị của m để hai nghiệm của pt đã cho thỏa (x1 – x2)2 = x1 – 3×2.

° Lời giải:

a) Ta có: 

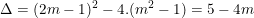
– Phương trình có 2 nghiệm phân biệt khi chỉ khi:

b) Phương trình có 2 nghiệm khi chỉ khi m<5/4.

– Áp dụng Vi-ét, ta có: 

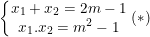
– Theo bài ra: (x1 – x2)2 = x1 – 3×2

 ⇔ (x1 + x2)2 – 4x1x2 = x1 – 3×2 

 ⇔ (2m – 1)2 – 4(m2 – 1) = x1 – 3×2 

 ⇔ x1 – 3×2 = 5 – 4m (**)

– Từ pt thứ nhất trong hệ (*) với (**) ta có hệ pt:

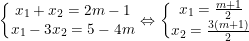
– Mặt khác, lại có: x1x2 = m2 – 1 

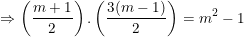
– Đối chiếu với điều kiện m<5/4 thấy m = 1 và m = -1 đều thỏa mãn (x1 – x2)2 = x1 – 3×2.

⇒ Kết luận: Với m = 1 hoặc m = -1 hì pt đã cho có 2 nghiệm thỏa mãn 

• Hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào m;

 Bước 1: Tìm điều kiện để phương trình có hai nghiệm phân biệt.

 Bước 2:  Áp dụng Vi-ét tính x1 + x2 và x1.x2 

 Bước 3: Biến đổi kết quả để không phụ thuộc tham số (không còn tham số)

* Ví dụ: Cho phương trình x2 – 2(m – 1)x + m – 3 = 0 (m là tham số)

a) CMR phương trình đã cho luôn có 2 nghiệm phân biệt.

b) Tìm một hệ thức liên hệ giữa 2 nghiệm của pt đã cho mà không phụ thuộc vào m.

c) Tìm giá trị nhỏ nhất của 

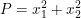
 (với x1, x2 là nghiệm của pt đã cho)

° Lời giải:

a) Ta có: 

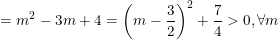
– Vậy phương trình đã cho luôn có 2 nghiệm phân biệt.

b) Theo hệ thức Vi-ét, ta có:

 (không phụ thuộc vào m).

c) Ta có: 

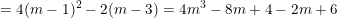
– Do đó:

 dấu “=” xảy ra khi 

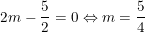
⇒ Kết luận: Pmin = 15/4 khi m = 5/4.

• So sánh nghiệm của phương trình bậc hai với một số bất kỳ:

 Bước 1: Tìm điều kiện phương trình có nghiệm (Δ ≥ 0).

 Bước 2: Áp dụng Vi-ét tính x1 + x2 và x1.x2 

 +) Với bài toán: Tìm m để phương trình có nghiệm lớn hơn α (x1 > x2 > α)

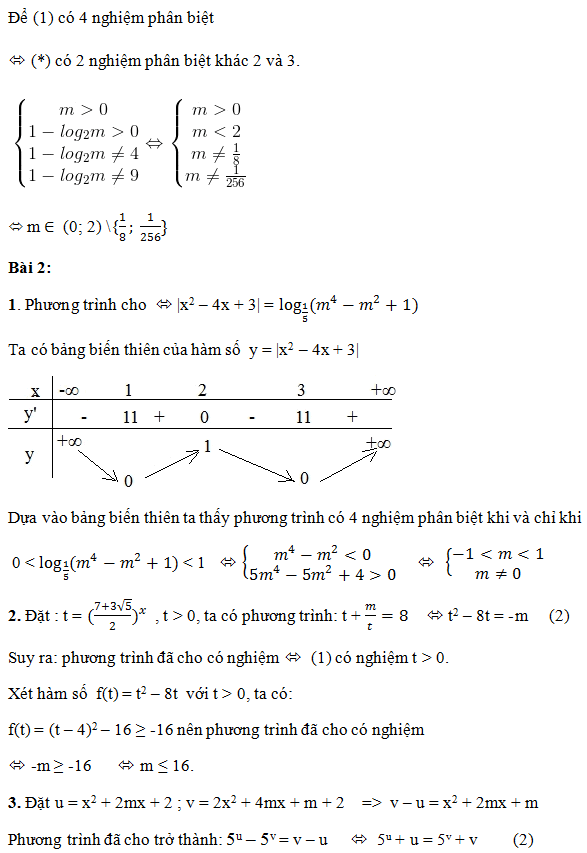
 Thay biểu thức Vi-ét vào hệ để tìm m

 +) Với bài toán: Tìm m để phương trình có 2 nghiệm nhỏ hơn α (x1 < x2 < α)

  Thay biểu thức Vi-ét vào hệ để tìm m

  +) Với bài toán: Tìm m để phương trình có nghiệm sao cho x1 < α < x2

  Thay biểu thức Vi-ét vào hệ để tìm m

* Ví dụ: Cho phương trình x2 -2(m – 1)x + 2m – 5 = 0 (m là tham số)

a) CMR phương trình luôn có 2 nghiệm phân biệt với mọi m

b) Tìm giá trị của m để phương trình có 2 nghiệm x1, x2 thỏa mãn x1 < 1 < x2.

° Lời giải:

a) Ta có: 

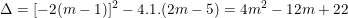
 Vậy PT luôn có 2 nghiệm phân biệt với mọi m.

b) Theo Vi-ét ta có: 

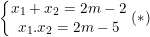
 Theo yêu cầu bài toán thì x1 < 1 < x2 

 Thay (*) và (**) ta được: (2m – 5) – (2m – 2) + 1 < 0

 ⇔ 0.m – 2 < 0 (đúng với mọi m).

Xem thêm: Chia Sẻ Khóa Học Photoshop Thùy Uyên, Học Photoshop Nâng Cao Cùng Thùy Uyên

⇒ Kết luận: Vậy với mọi m thì pt trên có 2 nghiệm x1, x2 thỏa  x1 < 1 < x2.