Dạng 2: Lập Phương Trình Tham Số Hyperbol, Dạng 2: Lập Phương Trình Của Hypebol (H)

Bài giảngGiải tích 1Giải tích 2Đại số tuyến tính (Linear Algebra)Xác suất thống kêVideo bài giảngThảo luậnThảo luận về giải tíchThảo luận ĐSTTThảo luận XSTKEbooksMaths Ebooks

1. Phương trình tham số của đường cong:

Cho hai hàm số:

Khi t thay đổi, điểm

vẽ nên đường cong (C) trong mặt phẳng tọa độ (Oxy).

Nếu từ (1) ta giải được t theo x ( t = t(x)) rồi thế vào (2) thì ta sẽ có phương trình của đường cong (C) : y = f(x).

Các hàm số {(1), (2)} được gọi là phương trình tham số của đường cong (C).

Đang xem: Phương trình tham số hyperbol

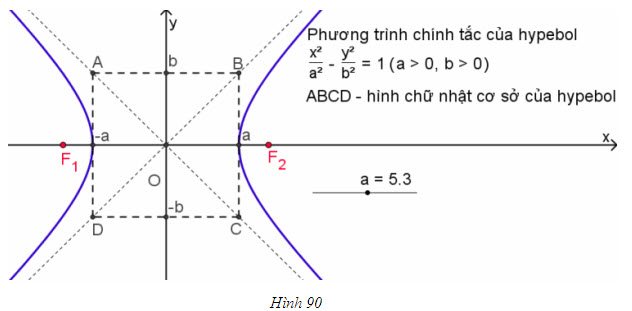
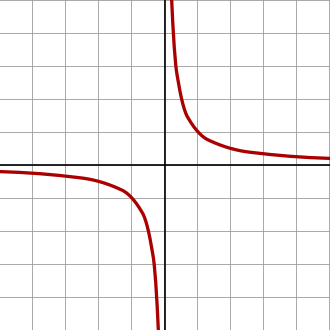
Ví dụ 1: Xét hyperbol (H):

Vì hiệu bình phương của

,

bằng 1, nên có thể coi chúng là cht và sht:

,

,

Vậy ta có phương trình tham số của Hyperbol là:

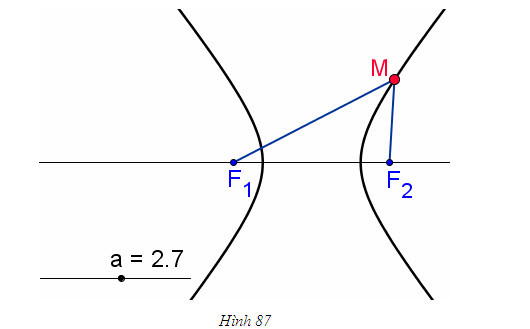
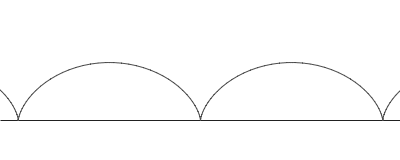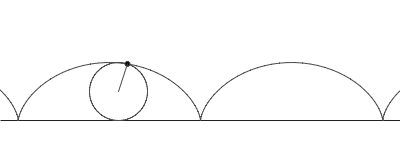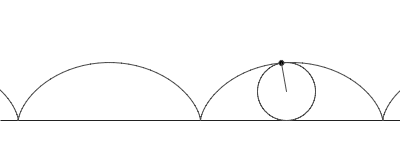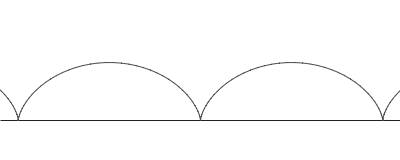
Ví dụ 2: Xicloit là quỹ đạo của một điểm M nằm trên một đường tròn bán kính a khi vòng tròn đó lăn không trượt trên một đường thẳng.

Giả sử vòng tròn lăn về phía hướng dương của trục Ox (và lăn trên trục hoành) , vị trí ban đầu của M trùng với gốc tọa độ O.

Khi đó, ta dễ dàng xác định được phương trình tham số của quỹ đạo điểm M là:

2. Khảo sát đường cong cho bằng tham số:

Việc khảo sát và vẽ đồ thị của đường cong tham số tiến hành tương tự như đã làm đối với đường cong có phương trình

. Gồm các bước sau đây:

Tìm miền xác định, tính chẵn lẻ, tuần hoàn.Khảo sát và lập bảng biến thiên:

Tính đạo hàm

Tìm các giá trị của tham số t sao cho tại đó ít nhất một trong các đạo hàm

hay

triệt tiêu. (nếu tồn tại

sao cho

,

thì điểm

là điểm kỳ dị, với

).

Mỗi khoảng

tương ứng với khoảng

sẽ xác định dấu của y”(x).

Tính đạo hàm cấp 2:

}^3}} = { \dfrac{{\ddot{y}}.{\dot{x}} – {\ddot{x}}.{\dot{y}}}{{\dot{x}}^3} } \qquad (4)” class=”latex” />

Từ (4) ta tìm các giá trị để đạo hàm cấp 2 triệt tiêu, từ đó xác định khoảng lồi, lõm của đường cong.Tìm tiệm cận của đường cong:

Nếu

,

thì x = a là tiệm cận đứng.

Xem thêm: Cách Tìm Nghiệm Trên Máy Tính Fx 570Vn Plus, 570Es Plus, Giải Toán Bằng Máy Tính Casio Fx 570Vn Plus

Nếu

,

thì y = b là tiệm cận ngang.

Nếu khi

,

,

và:

,

= b ” class=”latex” />

thì y = ax + b là tiệm cận xiên.

3. Các ví dụ minh họa:

Ví dụ 1: Khảo sát và vẽ đường cong cho bởi phương trình:

Các hàm số x(t), y(t) xác định với mọi t.

Nhưng vì các hàm số

là các hàm số tuần hoàn với chu kỳ 2

nên ta chỉ cần khảo sát với t nằm trong đoạn <0;2

>.

Do đó, khoảng biến thiên của x là đoạn <-a; a> và khoảng biến thiên của y là đoạn <-a; a>.

Vậy đường cong được khảo sát không có tiệm cận.

Xét khoảng biến thiên. Ta có:

khi

khi

khi t = 0,

tại

Ta có bảng biến thiên sau:

Tính đạo hàm cấp hai ta có:

Do đó:

Nhận thấy:

Khi

Khi

: thì

nên đường cong nằm trong góc phần tư thứ nhất

Khi

: thì

nên đường cong nằm trong góc phần tư thứ hai.

Khi

: thì

nên đường cong nằm trong góc phần tư thứ ba.

Xem thêm: Hướng Dẫn Cách Xuống Dòng Trong Excel Và Google Spreadsheets Dễ Đơn Giản Nhất

Khi

: thì

nên đường cong nằm trong góc phần tư thứ tư.

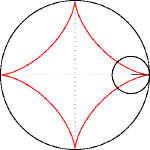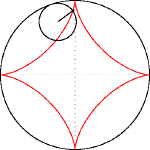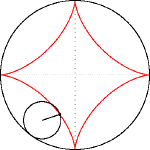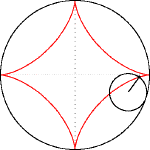
Từ những dữ liệu trên ta sẽ có đường cong (C) trong mặt phằng là đường màu đỏ trong hình sau:

Phương trình đường cong (C) có được bằng cách lăn đường tròn nhỏ, bán kính a/4 bên tròn đường tròn lớn, bán kính a theo hướng ngược chiều kim đồng hồ, bắt đầu từ điểm (1;0)

thầy ơi thầy cho em hỏi, trong toạ độ cực thì vi phân ds được tính theo công thức nào? và trong toạ độ cầu thì dv được tính theo công thức nào ah?(Em biết công thức tính nhưng em không nhớ cách chứng minh thế nào?)hihi…sách vở năm nhất em “quăng” mất rồi…Thầy ạh, em khi học về phần cơ lý thuyết em có học về tenser, nhưng chỉ là ứng dụng cho mooment quán tính, thầy có tài liệu nào về tensor và ứng dụng của nó cho vật lý nữa không ạh? Em muốn tìm cách ứng dụng tensor vào việc học môn điện động lực thay vì phải dùng định lý Gauss hay chia nhỏ vật ra thành những vi phân vô cùng nhỏ rồi lấy tích phân toàn bộ vật.(vì em thấy có một sự tương ứng giữa việc dùng tensor và chia nhỏ vật ra thành những vi phân…)em cảm ơn thầy ạh…