Chuyên Đề Bất Phương Trình Bậc Nhất Một Ẩn Lớp 8, Chuyên Đề: Bất Phương Trình Bậc Nhất Một Ẩn

1. Bất đẳng thức

Ta gọi hệ thức $ ab;$ $ age b;$ $ ale b$) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức. Đang xem: Chuyên đề bất phương trình bậc nhất một ẩn

2. Liên hệ giữa thứ tự và phép cộng

– Nếu $ a – Nếu $ a>b$ thì $ a+c>b+c$ – Nếu $ ale b$ thì $ a+cle b+c$ – Nếu $ age b$ thì $ a+cge b+c$ Khi cộng cùng một số vào cả hai vế của một bất đẳng thức thì được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho

Ví dụ: Cho $ a>bRightarrow a+3>b+3$

3. Liên hệ giữa thứ tự và phép nhân

Khi nhân cả hai vế của bất đẳng thức với cùng một số dương thì được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho. Với ba số a, b, c mà $ c>0$ ta có: – Nếu $ ab$ thì $ ac>bc;$ nếu $ age b$ thì $ acge bc$ Khi nhân cả hai vế của bất đẳng thức với cùng một số âm thì được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho. Với ba số a, b, c mà $ cbc;$ nếu $ ale b$ thì $ acge bc$ – Nếu $ a>b$ thì $ ac

Ví dụ: $ a>bRightarrow a.(-3)4. Bất phương trình một ẩn

4.1 Nghiệm của bất phương trình

$ x=a$ gọi là nghiệm của bất phương trình nếu ta thay $ x=a$ vào hai vế của bất phương trình thì được một bất đẳng thức đúng

Ví dụ: x = 3 là nghiệm của bất phương trình $ 2x+34.2 Tập nghiệm của bất phương trình

Tập nghiệm của bất phương trình là tập tất cả các giá trị của biến x thỏa mãn bất phương trình.

4.3 Biểu diễn tập nghiệm

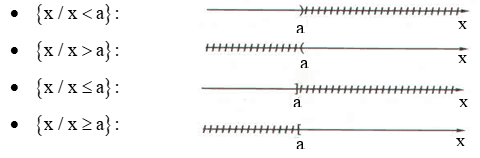
5. Bất phương trình bậc nhất một ẩn

Hai bất phương trình có cùng tập nghiệm là hai bất phương trình tương đương.

5.1 Bất phương trình tương đương

Ví dụ: Hai bất phương trình $ 2x+1>0$ và $ x>-frac{1}{2}$ là hai bất phương trình tương đương.

Xem thêm: Giáo Án Dạy Trẻ Làm Đồ Chơi Từ Phế Liệu Đơn Giản, Làm Đồ Dùng Đồ Chơi Từ Chai Nhựa

5.2 Quy tắc chuyển vế

Khi chuyển vế một hạng tử từ vế này sang vế kia của bất phương trình phải đổi dấu hạng tử đó.

Ví dụ: $ x+35.3 Quy tắc nhân

Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:; – Giữ nguyên chiều bất đẳng thức nếu đó là số dương – Đổi chiều bất đẳng thức nếu đó là số âm. Xem thêm: Hướng Dẫn Cách Lập Bảng Thống Kê Số Lượng Trong Excel, Cách Tạo Bảng Thống Kê Mô Tả Số Liệu Trong Excel

Ví dụ: $ -x>-3Leftrightarrow x6. Phương trình chứa dấu giá trị tuyệt đối

– Áp dụng định nghĩa giá trị tuyệt đối: – Giải phương trình không có dấu giá trị tuyệt đối – Chọn nghiệm thích hợp trong trường hợp đang xét – Tính chất: $ left| x ight|ge 0;$ $ left| {-x} ight|=left| x ight|;$ $ {{left| x ight|}^{2}}={{x}^{2}}$

Ví dụ: $ left| {2x}
ight|=x-6$

– Với $ xge 0$ ta có: $ left| {2x}
ight|=x-6Leftrightarrow 2x=x-6Leftrightarrow x=-6$ (loại)

– Với $ xb,$ so sánh:

a) $ a-7$ và $ b-7$ c) $ a+30$ và $ b+30$ e) $ a-15$ và $ b-15$

b) $ 6a$ và $ 6b$ d) $ -5a$ và $ -5b$ f) $ a+5$ và $ b+3$

Bài toán 2: So sánh a và b nếu:

a) $ a-7le b-7$ d) $ 35+age 35+b$ g) $ a+13>b+13$

b) $ -5a$ -14b+7$ i) $ 2a0,b>0$ và $ a>b$. Chứng tỏ rằng $ frac{1}{a}1$

c) $ frac{1}{{15}}2x+1$ c) $ 7-3xx+1$ d) $ 5left( {x-2}
ight)>3x-1$

Bài toán 9: Kiểm tra xem $ x=-2$ có là nghiệm của bất phương trình sau không?

a) $ 3x+5>-9$ c) $ 10-4x>7x-12$

b) $ -5×4$ c) $ xge -1$ e) $ x>7$ g) $ xge -2$

b) $ x7$

c) $ left| x
ight|le 2$ d) $ left| x
ight|ge 9$

Bài toán 12: Viết bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau:

a) Tổng của một số nào đó và 11 lớn hơn 17;

b) Hiệu của 15 và một số nào đó nhỏ hơn – 13;

c) Tổng của 3 lần số đó và 7 lớn hơn 8;

d) Hiệu của 10 và 5 lần số đó nhỏ hơn 15;

e) Tổng hai lần số đó và số 3 thì lớn hơn 18;

f) Hiệu của 5 và 3 lần số nào đó nhỏ hơn hoặc bằng 10.

Bài toán 13: Chứng minh các bất phương trình sau:

a) $ {{x}^{2}}+x+1>0$ có nghiệm c) $ left( {x-1}
ight)left( {x-5}
ight)+10

1. $ x+7>-3$ 16. $ 3x-6>x$ 2. $ x+175$ 19. $ 4{{left( {x-3}
ight)}^{3}}-{{left( {2x-1}
ight)}^{2}}ge 12x$ 5. $ 5x+18>0$ 20. $ 2x-xleft( {3x+1}
ight)2left( {x-1}
ight)+x$ 7. $ 9-2x8x-2$ 8. $ -11-3xge 0$ 23. $ 1+x-frac{{x-3}}{4}>frac{{x+1}}{4}-frac{{x-2}}{3}$ 9. $ -3x>-4x+7$ 24. $ 2{{x}^{2}}+2x+1-frac{{15left( {x-1}
ight)}}{2}ge 2xleft( {x+1}
ight)$ 10. $ 4x+28x-2$ 11. $ 5×0$ 12. $ -6x-3>-7x+9$ 27. $ 2{{x}^{3}}>x+1$ 13. $ 5x

Bài toán 15: Giải các bất phương trình sau (a là số cho trước):

a) $ 2x-3age 0$

b) $ a+1-5xge 0$

c) $ left( {a-1}
ight)x+2a+1>0$ với $ a>1$

d) $ left( {2a+1}
ight)x-1-age 0$ với $ a

1. $ left| {2x-5}
ight|=2-x$ 11. $ left| {3-2x}
ight|=3x-7$ 2. $ left| {2x-7}
ight|=17-x$ 12. $ left| {frac{x}{2}-frac{5}{4}}
ight|=x-1$ 3. $ left| {3x-2}
ight|=1-x$ 13. $ left| {x+2}
ight|=2left( {3-x}
ight)$ 4. $ left| {2x-3}
ight|=x$ 14. $ left| {3x}
ight|-x-4=0$ 5. $ left| {3x}
ight|=x+7$ 15. $ left| {6-x}
ight|=2x-3$ 6. $ left| {5x}
ight|=3x+8$ 16. $ 9-left| {-5x}
ight|+2x=0$ 7. $ left| {-4,5x}
ight|=6+2,5x$ 17. $ {{left( {x+1}
ight)}^{2}}+left| {x+10}
ight|-{{x}^{2}}-12=0$ 8. $ left| {-4x}
ight|=-2x+11$ 18. $ left| {4-x}
ight|+{{x}^{2}}-left( {5+x}
ight)x=0$ 9. $ left| {x-9}
ight|=2x+5$ 19. $ 10x-10+left| {3x-5}
ight|-5left( {2x-3}
ight)=0$ 10. $ left| {3x-1}
ight|=4x+1$ 20. $ {{left( {x-2}
ight)}^{2}}+left| {x-5}
ight|-{{x}^{2}}-14=0$

Bài toán 25: Giải phương trình

a) $ frac{{left| x
ight|-1}}{4}-frac{1}{8}left( {frac{{left| x
ight|-5}}{4}-frac{{14-2left| x
ight|}}{5}}
ight)=frac{{left| x
ight|-9}}{2}-frac{7}{8}$

b) $ frac{{7x+5}}{5}-x=frac{{left| {3x-5}
ight|}}{2}$

c) $ x-frac{{left| {3x-2}
ight|}}{5}=3-frac{{2x-5}}{3}$

Bài toán 26: Giải phương trình

a) $ {{x}^{2}}-left| x
ight|=6$ e) $ left| {x+1}
ight|-left| {2-x}
ight|=0$

b) $ left| {{{x}^{2}}-4}
ight|={{x}^{2}}-4$ f) $ left| x
ight|-left| {x-2}
ight|=2$

c) $ left| {2x-{{x}^{2}}-1}
ight|=2x-{{x}^{2}}-1$ g) $ left| {x-1}
ight|+left| {x-2}
ight|=1$

d) $ left| {{{x}^{2}}-3x+3}
ight|=3x-{{x}^{2}}-1$ h) $ left| {x-2}
ight|+left| {x-3}
ight|+left| {2x-8}
ight|=9$

Bài toán 27: Giải phương trình

a) $ 3xleft| {x+1}
ight|-2xleft| {x+2}
ight|=12$

b) $ frac{{{{x}^{2}}-4-left| {x-2}
ight|}}{2}=xleft( {x+1}
ight)$

c) $ frac{{{{x}^{3}}+{{x}^{2}}-x}}{{xleft| {x-2}
ight|}}=1$

d) $ frac{7}{{8x}}+frac{{5-x}}{{4{{x}^{2}}-8x}}=frac{{x-1}}{{2xleft( {x-2}
ight)}}+frac{1}{{8x-16}}$

e) $ frac{{x+2}}{{{{x}^{2}}+2x+4}}-frac{{x-2}}{{{{x}^{2}}-2x+4}}=frac{6}{{xleft( {{{x}^{4}}+4{{x}^{2}}+16}
ight)}}$

f) $ frac{{{{x}^{2}}-x}}{{x+3}}-frac{{{{x}^{2}}}}{{x-3}}=frac{{7{{x}^{2}}-3x}}{{9-{{x}^{2}}}}$

Bài toán 28: Giải bất phương trình

a) $ left| {2x+5}
ight|le left| {7-4x}
ight|$

b) $ left| {frac{{2-3left| x
ight|}}{{1+x}}}
ight|le 1$

c) $ frac{{left| {{{x}^{2}}-4x}
ight|+3}}{{{{x}^{2}}+left| {x-5}
ight|}}ge 1$

d) $ frac{9}{{left| {x-5}
ight|-3}}ge left| {x-3}
ight|$

e) $ left| {2x-1}
ight|ge x-1$

f) $ left| {2x+5}
ight|>left| {7-4x}
ight|$

Bài toán 29: Giải và biện luận bất phương trình

a) $ -1le frac{{x+m}}{{mx+1}}le 1$ b) $ frac{{x-m}}{{x+1}}=frac{{x-2}}{{x-1}}$ c) $ frac{{ax-1}}{{x–1}}+frac{b}{{x+1}}=frac{{aleft( {{{x}^{2}}+1}
ight)}}{{{{x}^{2}}-1}}$

Bài toán 30: Chứng minh các bất đẳng thức

a) $ {{a}^{2}}+{{b}^{2}}ge frac{1}{2}$ với $ a+b=1;$

b) $ {{a}^{2}}+{{b}^{2}}+{{c}^{2}}ge frac{1}{3}$ với $ a+b+c=1$

c) $ {{a}_{1}}^{2}+{{a}_{2}}^{2}+…+{{a}_{n}}^{2}ge frac{1}{n}$ với $ {{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}=1$

Bài toán 31: Cho biểu thức

$ M=left< {frac{{3left( {x+2} ight)}}{{2left( {{{x}^{3}}+{{x}^{2}}+x+1} ight)}}+frac{{2{{x}^{2}}-x-10}}{{2left( {{{x}^{3}}+{{x}^{2}}+x+1} ight)}}} ight>:left< {frac{5}{{{{x}^{2}}+1}}+frac{3}{{2left( {x+1} ight)}}-frac{3}{{2left( {x-1} ight)}}} ight>.frac{2}{{x-1}}$

a) Rút gọn M;

b) Tính giá trị của M biết $ left| x
ight|=frac{1}{3};$

c) Tìm x biết $ left| M
ight|=2004;$

d) Tìm giá trị của x để $ M>0,$ $ MSeries Navigation>”>Hình học 8 – Chuyên đề 1 – Hình thang, hình thang cân >>